More Information
Submitted: January 17, 2025 | Approved: February 06, 2025 | Published: February 07, 2025
How to cite this article: Sridhar LN. Bifurcations and control studies in Circadian Rhythms in Drosophila. Arch Case Rep. 2025; 9(2): 054-065. Available from:
https://dx.doi.org/10.29328/journal.acr.1001128
DOI: 10.29328/journal.acr.1001128
Copyright license: © 2025 Sridhar LN. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Bifurcation; Optimization; Control; Drosophila
Bifurcations and control studies in Circadian Rhythms in Drosophila
Lakshmi N Sridhar*
Chemical Engineering Department, University of Puerto Rico, Mayaguez, PR 00681, Puerto Rico
*Address for Correspondence: Lakshmi N Sridhar, Chemical Engineering Department, University of Puerto Rico, Mayaguez, PR 00681, Puerto Rico, Email: [email protected]
Bifurcation analysis and Multiobjective Nonlinear Model Predictive Control (MNLMPC) calculations were performed on a model of circadian oscillations of the period (PER) and timeless (TIM) proteins in Drosophila. The MATLAB program MATCONT was used to perform the bifurcation analysis. The optimization language PYOMO was used along with the state-of-the-art global optimization solvers IPOPT and BARON for the MNLMPC calculations. The bifurcation analysis revealed oscillation causing Hopf bifurcations while the MNLMPC calculations revealed the existence of spikes in the control profiles. Both Hopf bifurcation points and the control profile spikes were eliminated using an activation factor involving the hyperbolic tangent function.
Decroly, et al. [1] discovered the chaotic behavior in multiply regulated biochemical systems. Alamgir and Epstein [2] studied the oscillations in coupled chemical oscillators of the chlorite-bromate-iodide system. Aronson, et al. [3] studied the negative feedback defining a circadian clock. Baylies, et al. [4] conducted genetic, molecular, and cellular studies of the per locus and its products in Drosophila melanogaster. Crosthwaite, et al. [5] investigated the photo responses and the origins of circadian rhythmicity. Curtin, et al. [6] demonstrated how the temporally regulated nuclear entry of the Drosophila period protein contributes to the circadian clock. Dunlap [7] performed a genetic and molecular analysis of circadian rhythms. Edery, et al. [8.9] studied the phase shifting of the circadian clock by induction of the Drosophila period protein and its Temporal phosphorylation. Edmunds [10] discussed models and mechanisms for Circadian Timekeeping.
Eskin, et al. [11] investigated the requirement for protein synthesis to regulate the circadian rhythm by melatonin. Gekakis, et al. [12] demonstrated the Defective interaction between timeless protein and long-period mutant. Goldbeter [13] developed a model for circadian oscillations in the Drosophila period (PER) protein. Goldbeter [14] wrote a textbook in Biochemical Oscillations and Cellular Rhythms. Goodwin [15] minvestigated the oscillatory behavior in enzymatic control processes. Hall and co-workers [16-18] studied the molecular effects on biological rhythms. Hong and Tyson [19] investigated temperature compensation of the circadian rhythm in Drosophila based on dimerization of the PER protein. Huang, et al. [20] studied PER protein interactions and temperature compensation of a circadian clock in Drosophila. Khalsa, et al. [21] studied techniques for stopping the circadian pacemaker with inhibitors of protein synthesis Konopka and Benzer [22] investigated clock mutants of Drosophila melanogaster. Lee, et al. [23] discuss strategies for resetting the Drosophila clock by photic regulation of PER. and a PER-TIM complex. Leloup and Goldbeter [24] researched temperature compensation of circadian rhythms. Marus, et al. [25] studied the effect of constant light and circadian entrainment of perS flies. Myers, et al. [26] studied the light-induced degradation of timeless and entrainment of the Drosophila circadian clock. Qiu and Hardin [27] showed that the per mRNA cycling is locked to lights-off under photoperiodic conditions that support the circadian feedback loop function. Rosbash [28] studied the molecular control of circadian rhythms. Rutila, et al. [29] discuss t the timsl mutant of the Drosophila rhythm gene timeless manifests allele-specific interactions with period gene mutants. Saez and Young [30] discuss the regulation of nuclear entry of the Drosophila clock proteins period and timeless. Saunders, et al. [31] discuss the Light-pulse phase response curves for the locomotor activity rhythm in period mutants of Drosophila melanogaster. Sehgal, et al. [32] studied the loss of circadian behavioral rhythms and per RNA oscillations in the Drosophila mutant timeless. So and Rosbash [33] showed that post-transcriptional regulation contributes to Drosophila clock gene mRNA cycling. Taylor, et al. [34] demonstrate that inhibitors of protein synthesis on 80S ribosomes phase shift the Gonyaulax clock. Vosshall, et al. [35] show the existence of a block in nuclear localization of period protein by a second clock mutation, timeless. Young, et al. [36] discuss the molecular anatomy of a light-sensitive circadian pacemaker in Drosophila.
Zeng and co-workers [37,38] conducted further research about the Drosophila circadian clock. Reitz, et al. [39], Mia, et al. [40], Parcha, et al. [41] and Teeple, et al. [42] studied the relationships between obesity and Circadian rhythms, while Tobeiha, et al. [43] and Festus, et al. [44] studied the effects of cardiovascular health on Circadian rhythms.
Leloup JC, Goldbeter [45] developed a model for circadian rhythms in Drosophila incorporating the formation of a complex between the PER and TIM proteins. In this work a) bifurcation analysis is performed on the Leloup Goldeter model for circadian rhythms in Drosophila to identify and eliminate the Hopf bifurcations and b) Multiobjective NonlinearMmodel Predictive Control(MNLMPC) calculations are performed to ensure maximum production of the required product while simultaneously minimizing all the unwanted by-products.
Motivation and objectives
Circadian rhythms are endogenous limit cycle oscillations characterized for 24 hours. They constitute the biological rhythms with the longest period known to be generated at the molecular level. Oscillations are caused by Hopf bifurcation point. Limit cycle oscillations occur because of Hopf bifurcations. These bifurcations cause spikes in control profiles when one tries to control the process to achieve maximum benefit. These spikes hinder optimization and control tasks. The motivation of this work is to eliminate the limit cycle causing Hopf bifurcations and the spikes in control profiles when dynamic optimization tasks are performed. Hence, the main objectives of this work are a) Identify the Hopf bifurcation points computationally perform bifurcation analysis using MATCONT (a Matlab software for performing bifurcation analysis) b) Use an activation factor involving the tanh function to eliminate these Hopf bifurcation points c) Perform Multiobjective Nonlinear Model Predictive Control(MNLMPC) calculations for the Drosophila circadian rhythms model (Leloup Goldeter; [45]) d) Demonstrate the existence of spikes in the control profile when these calculations are performed) Use the tanh function’s activation factor to eliminate the control profile spikes. This paper is organized as follows. First, the Drosophila circadian rhythms model (Leloup Goldeter; [45]) details are presented. This is followed by describing the bifurcation analysis and Multiobjective Nonlinear Model Predictive Control(MNLMPC) procedures. The results and discussion section is then presented followed by the conclusions.
Drosophila circadian rhythms model
In this model, PER stands for period protein TIM stands for timeless protein. Mp, P0, P1, P2 stand for cytosolic concentration of PER mRNA, unphosphorylated PER, monophosphorylated PER and bisphosphorylated PER. MT, T0, T1, T2 stand for cytosolic concentration of TIM mRNA, unphosphorylated TIM, monophosphorylated TIM and bisphosphorylated. C represents the complex formed by the degradation of P2 and T2 while CN represents the nuclear form of the PER-TIM complex. The mRNAs are synthesized at rates of vSP, vST with rate constants Ksp, KsT. The subsequent degradation takes place at rates vmP, vmT with rate constants Kmp, KmT. kIp, k2p, k3p, k4p are the kinase rate constants while k1T, k2T, k3T, k4T are the phosphatase rate constants. v1p, v2p, v3p, v4p represents the maximum kinase rate while v1T, v2T, v3T, v4T represents the maximum phosphatase rate. More details can be found in Leloup and Goldeter [45]. The base parameter values are
The equations that constitute this model are
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
Bifurcation analysis
Multiple steady-states and oscillatory behavior occur in various situations. Multiple steady states occur because of t Branch and Limit bifurcation points cause multiple steady-states. Hopf bifurcation points produce oscillatory behavior. Ions and limit cycles. The MATLAB program MATCONT. (Dhooge Govearts, and Kuznetsov [46], Dhooge Govearts, Kuznetsov, Mestrom and Riet, [47]) is commonly used software to locate limit points, branch points, and Hopf bifurcation points. Consider an ODE system
(11)
x ∈ Rn . Defining the matrix A as
(12)
β is the bifurcation parameter. The matrix A can be written in a compact form as
(13)
The tangent at any point x; ( ) must satisfy
Av = 0 (14)
The matrix B must be singular at both limit and branch points. The n+1th component of the tangent vector Vn+1 = 0 at a limit point (LP) and for a branch point (BP) the matrix must be singular. At a Hopf bifurcation,
(15)
@ indicates the bialternate product while In is the n-square identity matrix. Hopf bifurcations cause unwanted oscillatory behavior and should be eliminated because oscillations make optimization and control tasks very difficult. More details can be found in Kuznetsov [48,49] and Govaerts [50].
Multiobjective nonlinear model predictive control
Flores Tlacuahuaz [51] first proposed the Multiobjective nonlinear model predictive control method that does not involve weighting functions, nor does it impose additional constraints on the problem unlike the weighted function or the epsilon correction method(Miettinen, [52]). For a a set of ODE
(16)
let (j = 12..n); be the variables that need to be minimized/maximized simultaneously, tf being the final time value, and n the total number of variables that need to be optimized simultaneously. In this MNLMPC method dynamic optimization problems that independently minimize/maximize each variable are solved individually. The minimization/maximization of each will lead to the values . Then the optimization problem that will be solved is
(17)
This will provide the control values for various times. The first obtained control value is implemented and the rest are ignored. The procedure is repeated until the implemented and the first obtained control values are the same or if the Utopia point ( ; for all j) is achieved. The optimization package in Python, Pyomo (Hart, et al. [53]), where the differential equations are automatically converted to algebraic equations will be used. The resulting optimization problem was solved using IPOPT (Wächter and Biegler [54]). The obtained solution is confirmed as a global solution with BARON (Tawarmalani, M. and N. V. Sahinidis [55]).
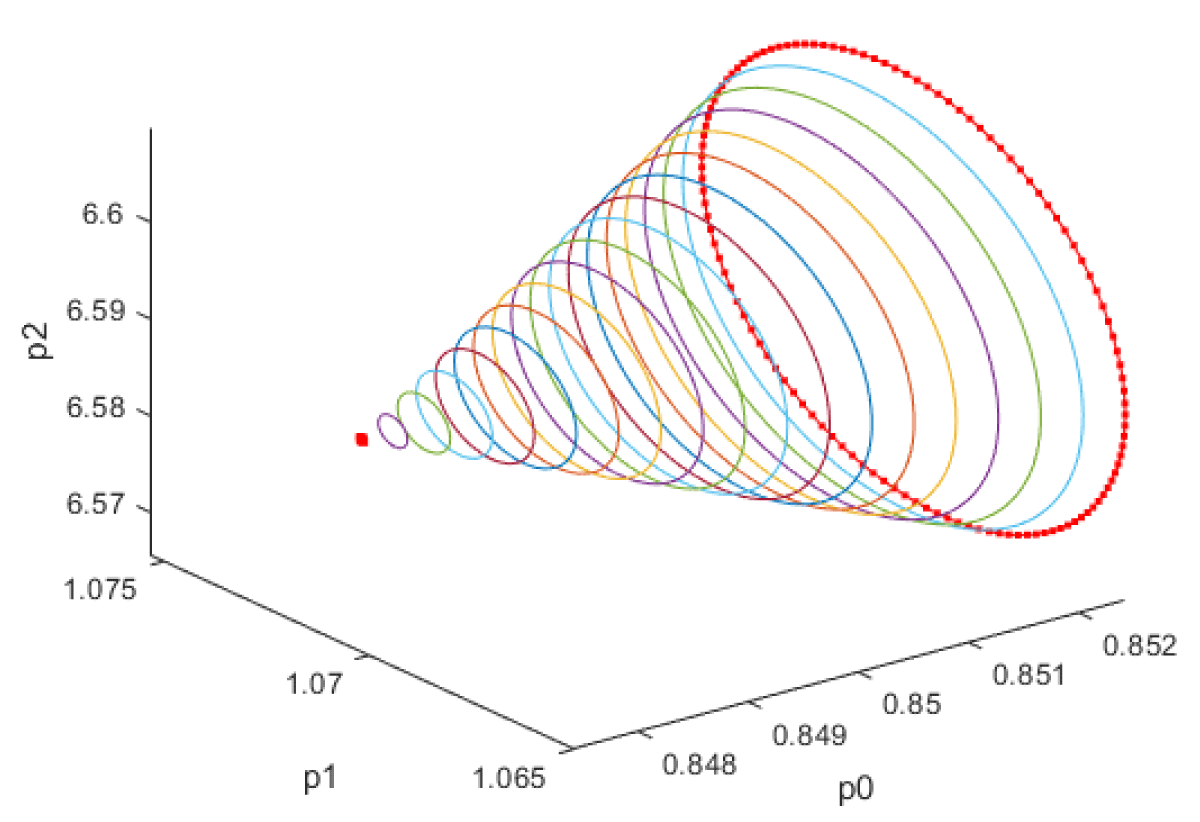
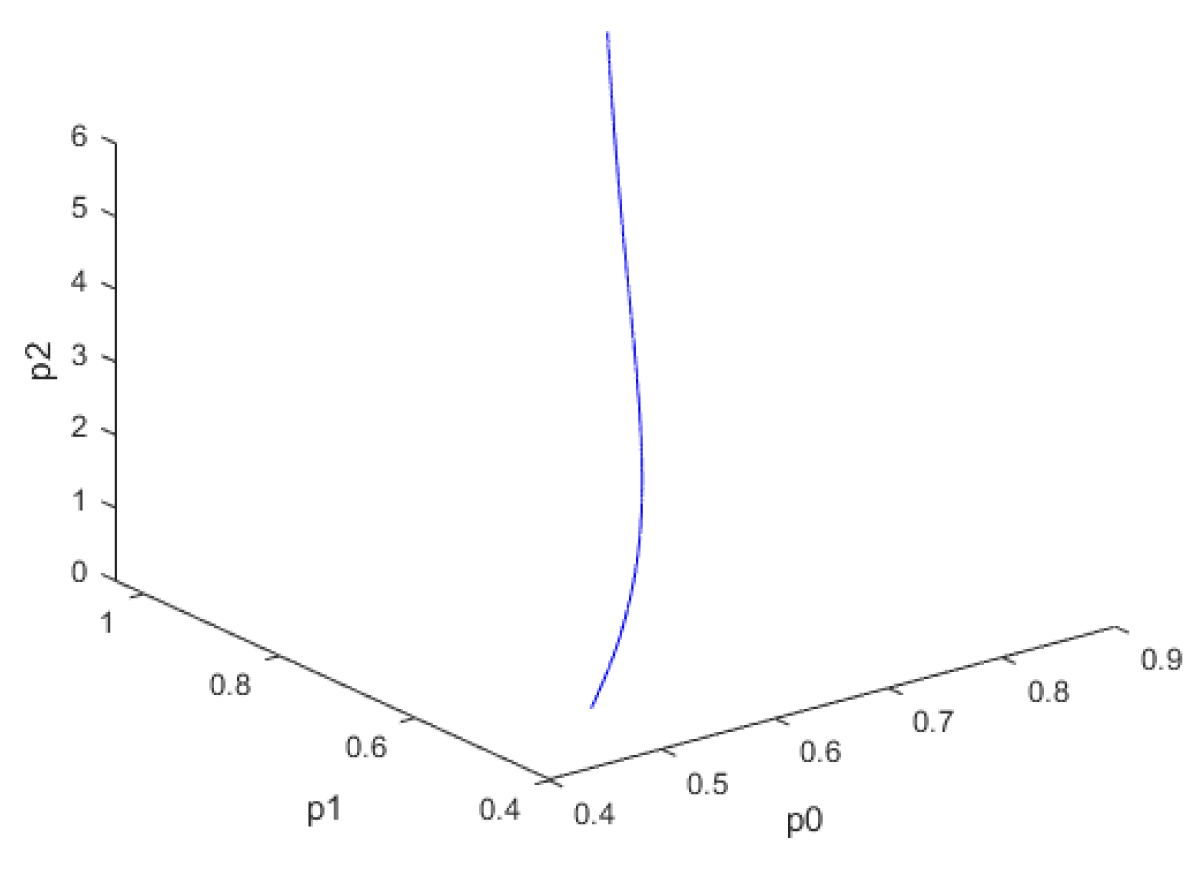
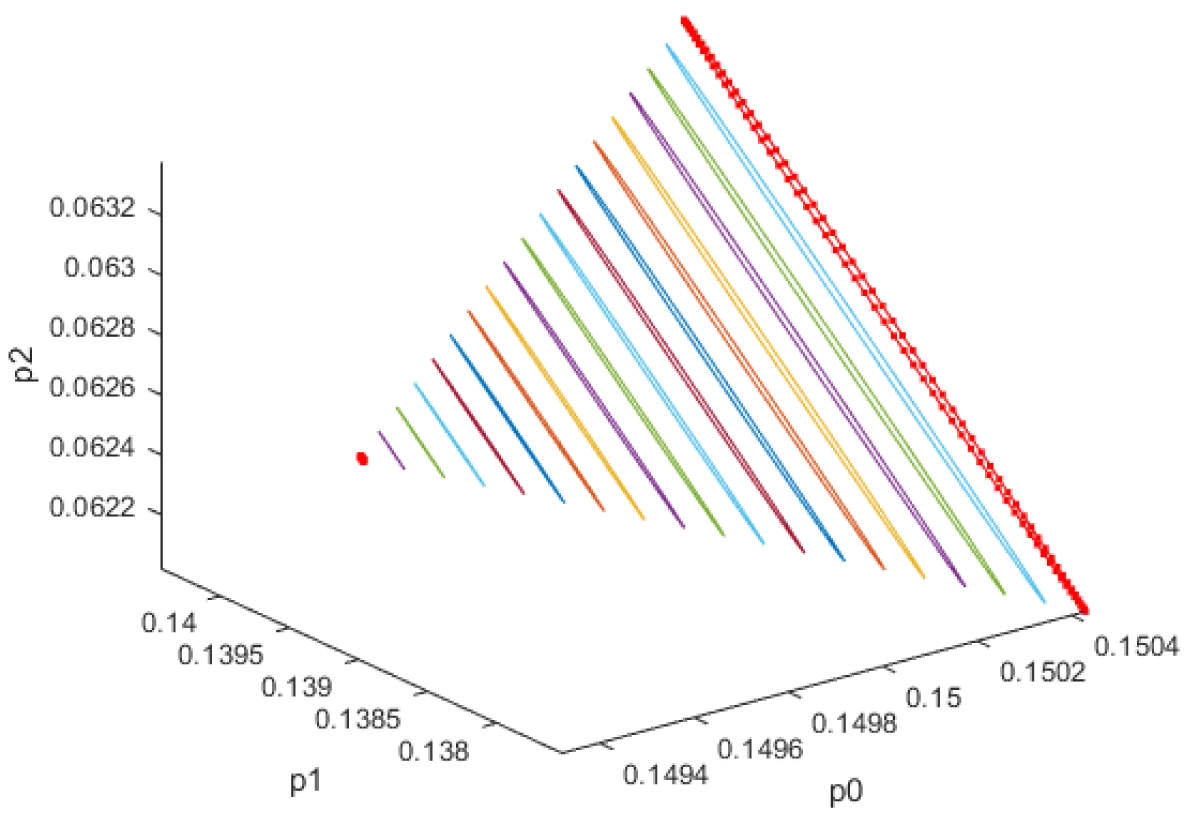
For the three bifurcation parameters kSp, kdN, vmP; the bifurcation analysis revealed Hopf bifurcation points that disappeared when the bifurcation parameters were modified with the activation factor involving the tanh function. The bifurcation parameters kSp, kdN, each resulted in one Hopf bifurcation point, while vmP resulted in two Hopf bifurcation points. The bifurcation parameters were treated as time dependent variables while the other parameters were the base parameters. Whenks ksP was the bifurcation parameter the Hopf bifurcation point was found at the point x = (Mp, P0, P1, P2, MT, T0, T1, T2, C, CN, ksP) = (0.311096 0.847336 1.070162 6.587611 0.311096 0.082204 0.076131 0.030362 0.375862 1.073892 6.559451). The limit cycle resulting from this Hopf bifurcation point is shown in Figure 1a. The Hopf bifurcation point and the limit cycle disappeared when ksP was modified to ksP tanh(ksP) / 10 (Figure 1b).
Figure 1a: Limit cycle when ksp is the bifurcation parameter.
Figure 1b: Hopf bifurcation point and limit cycle disappears when ksp is modified to ksp(tanh(ksp))/10.
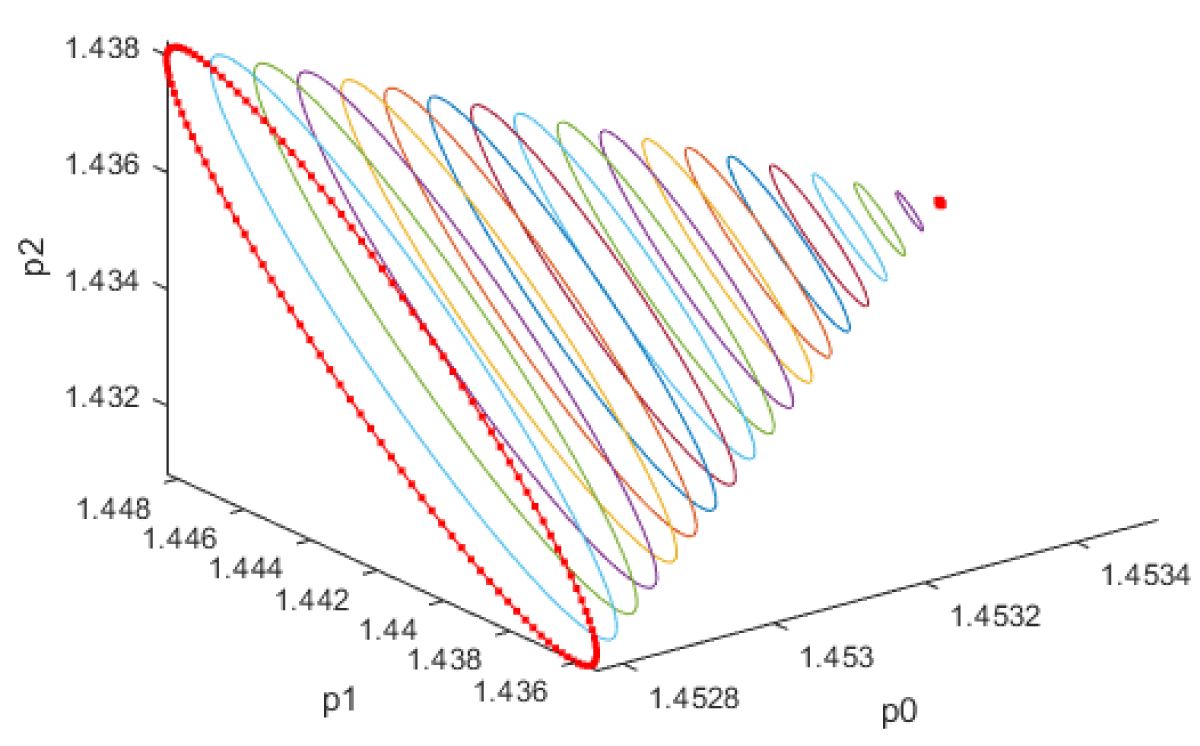
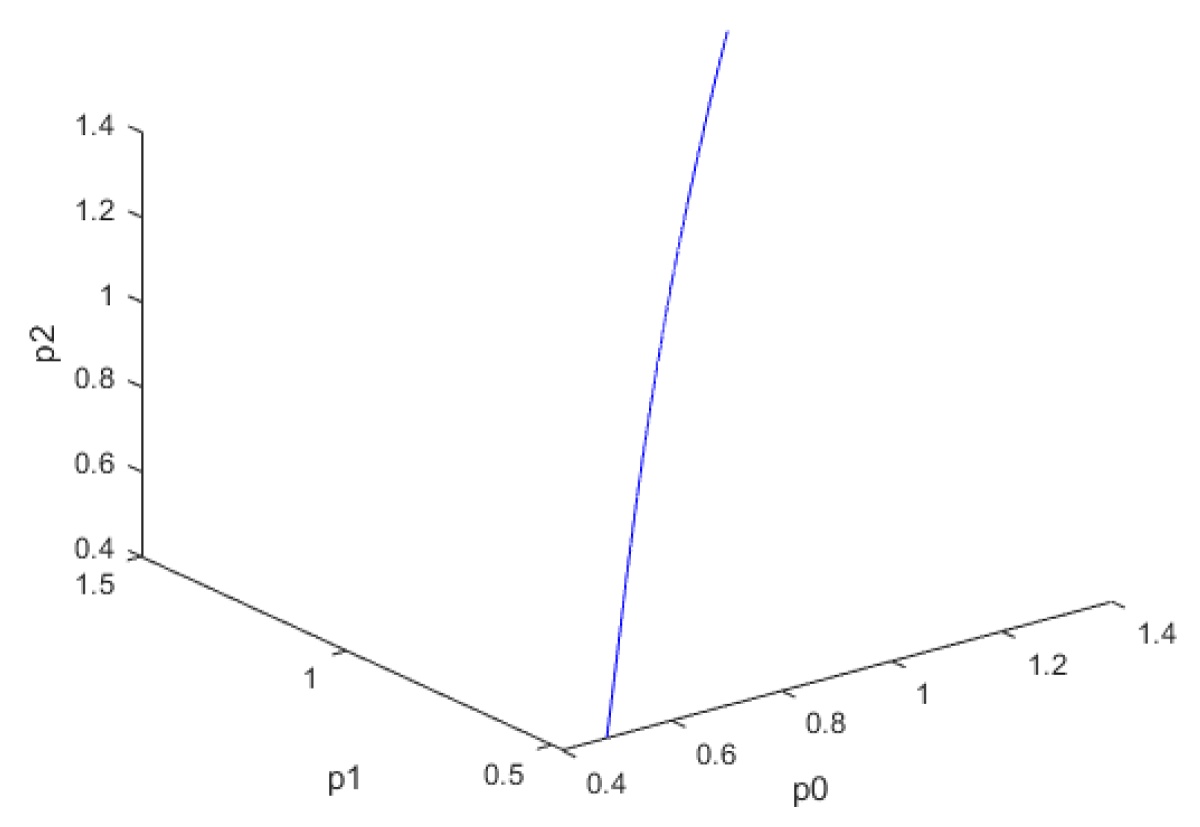
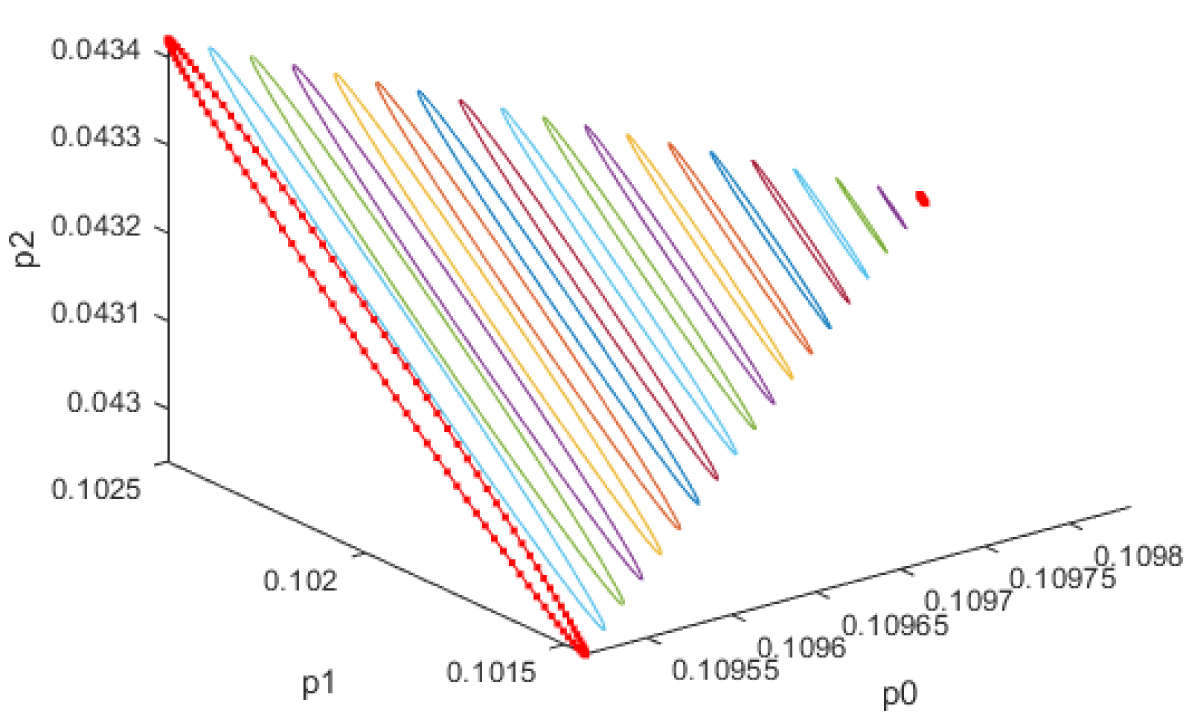
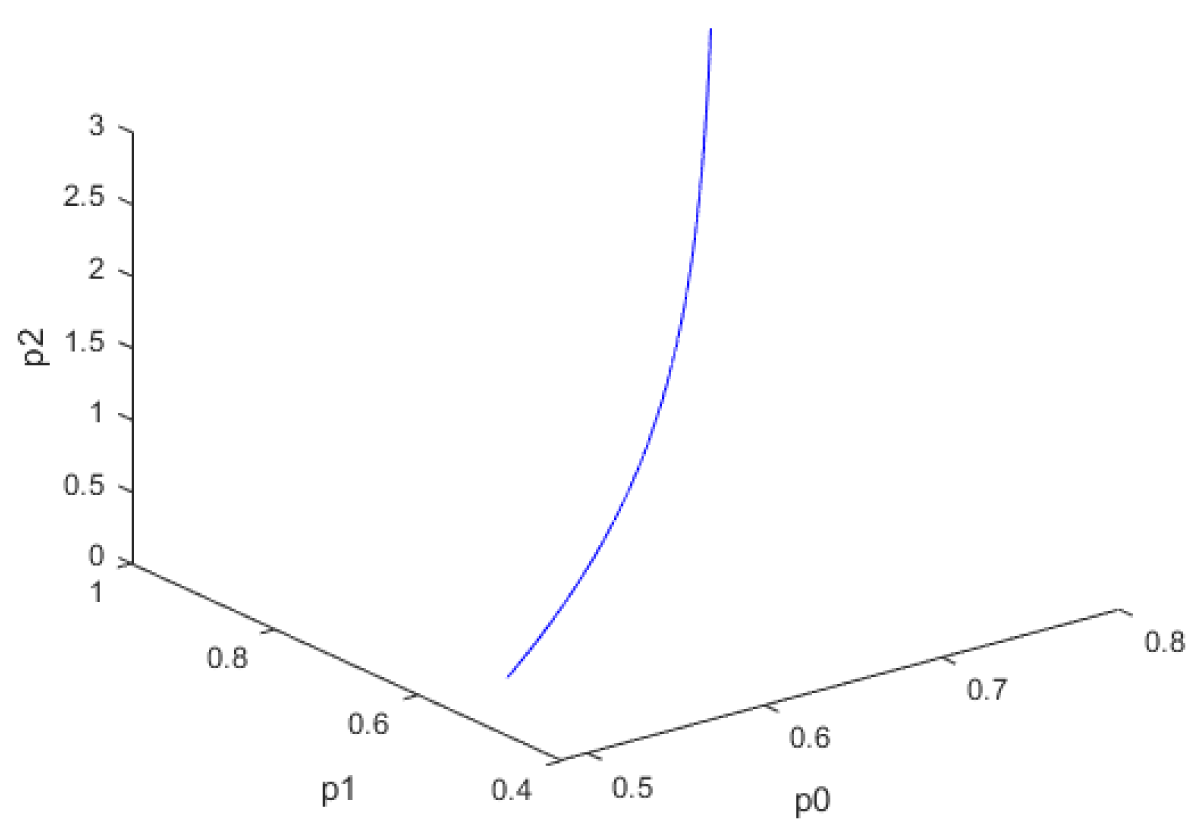
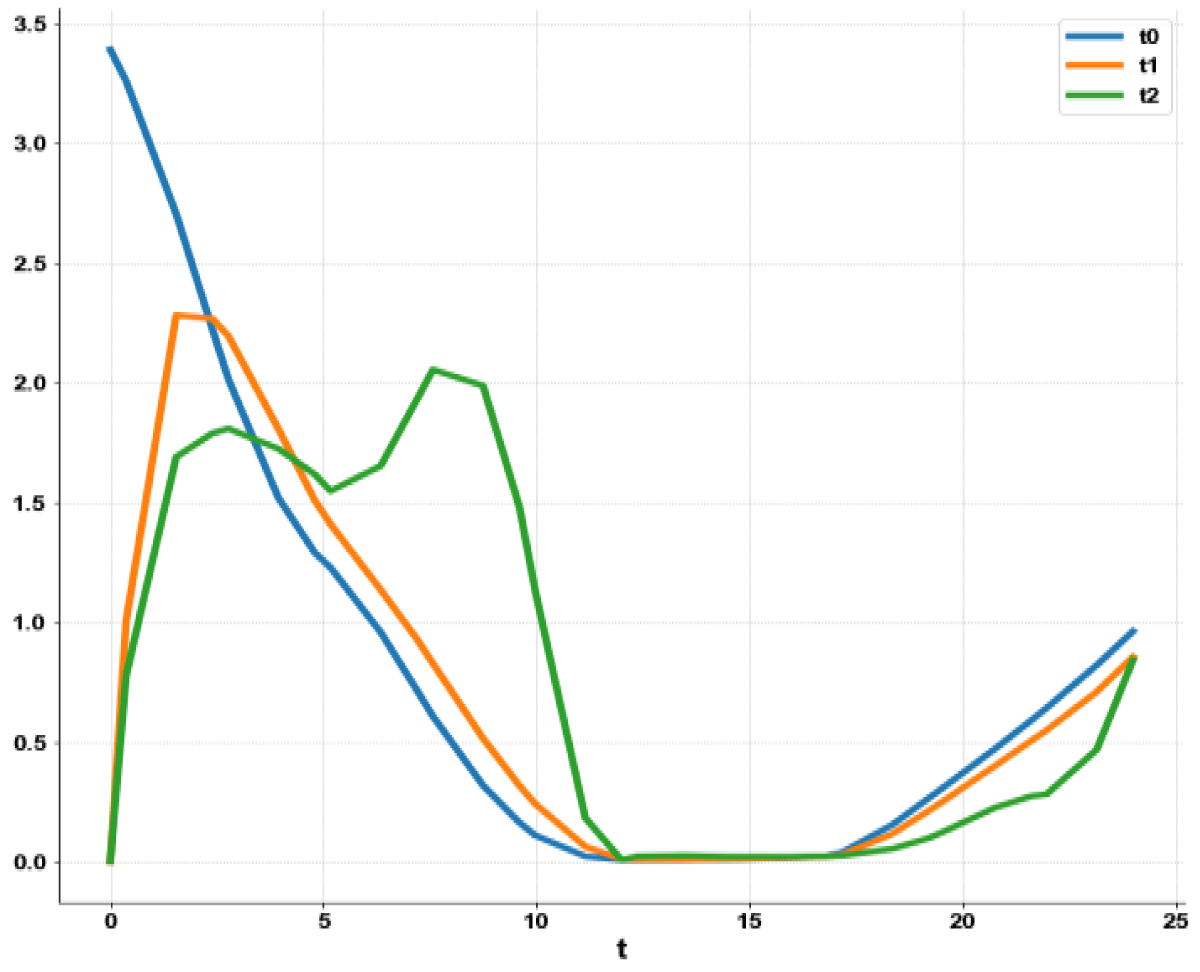
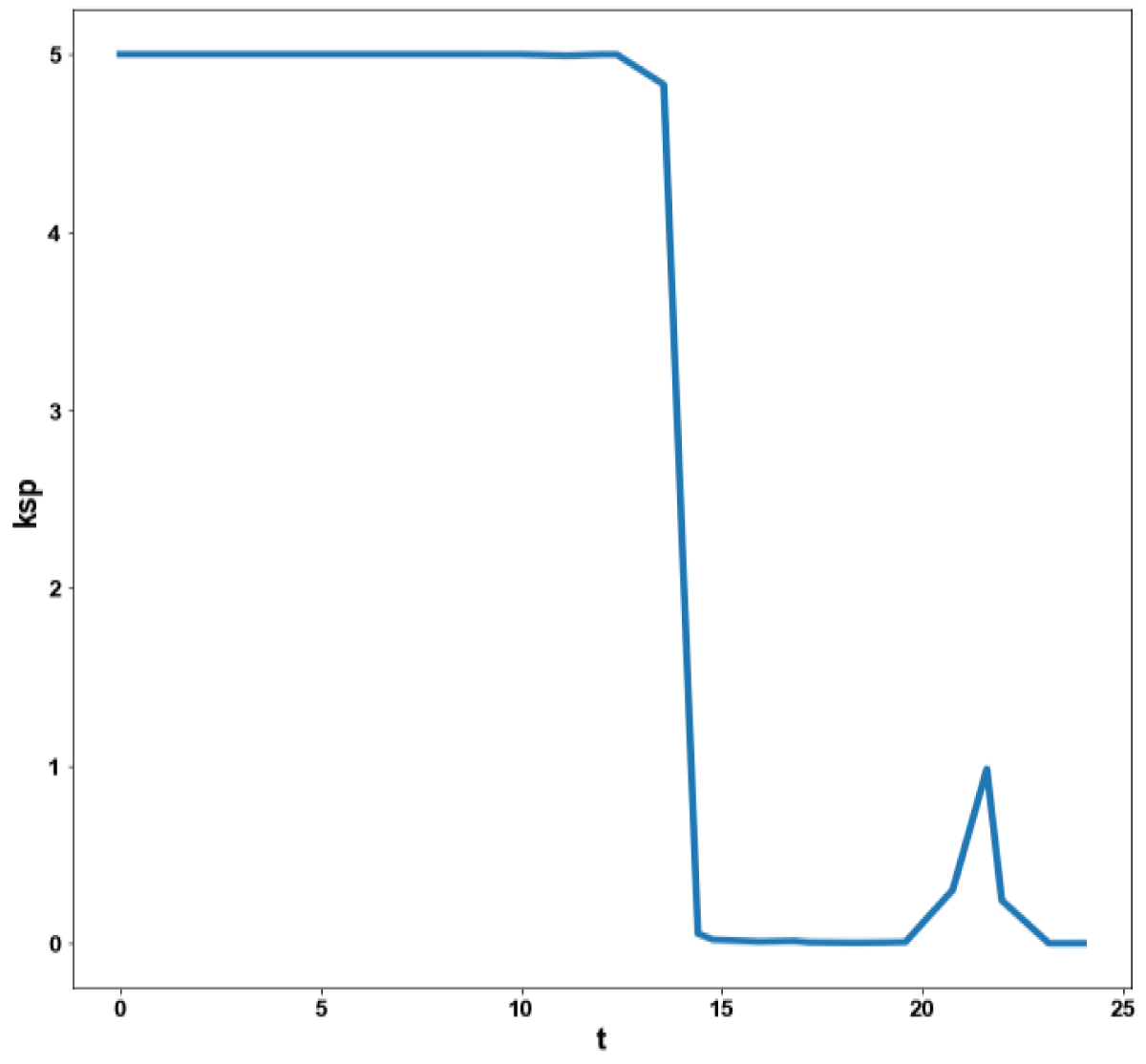
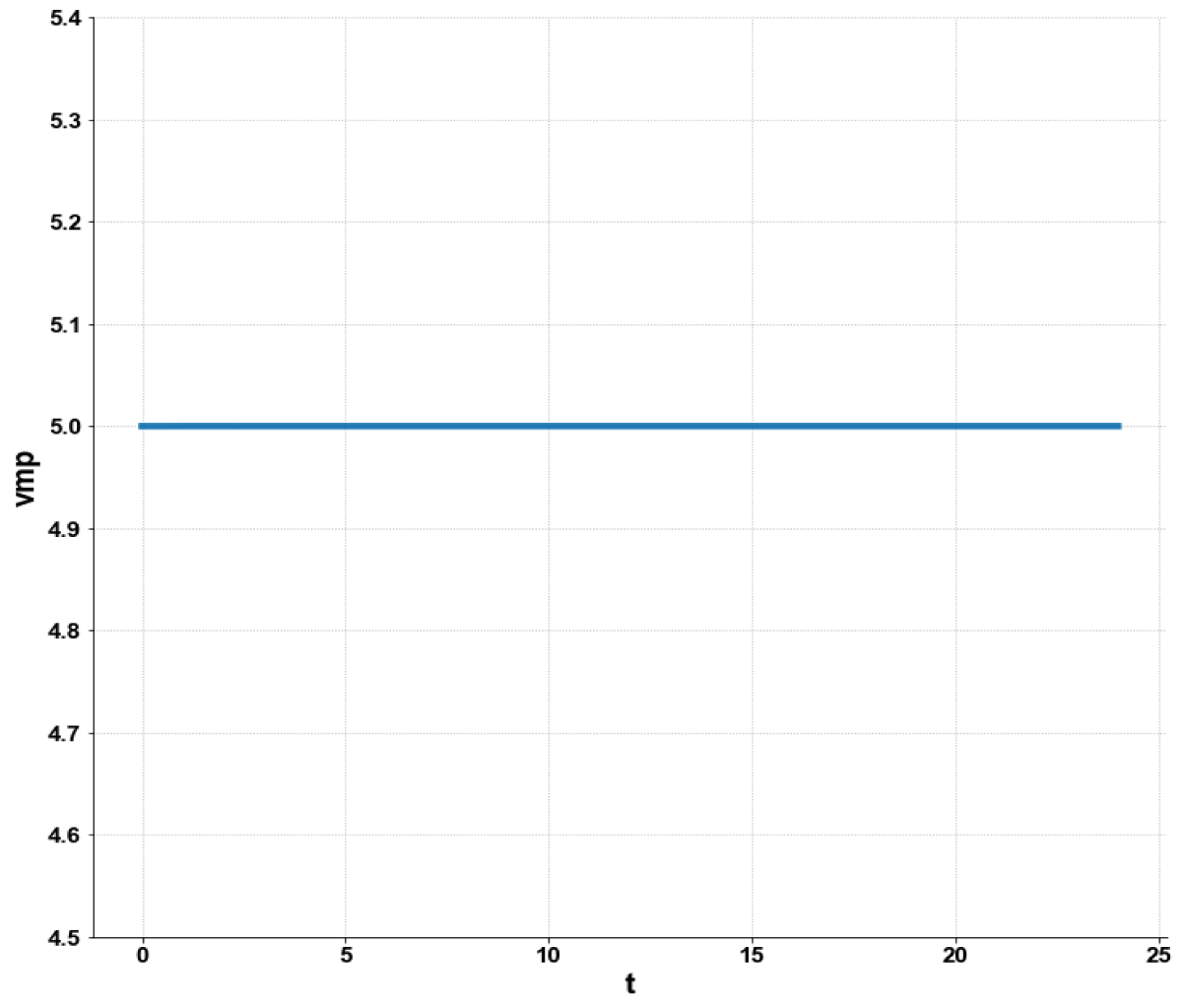
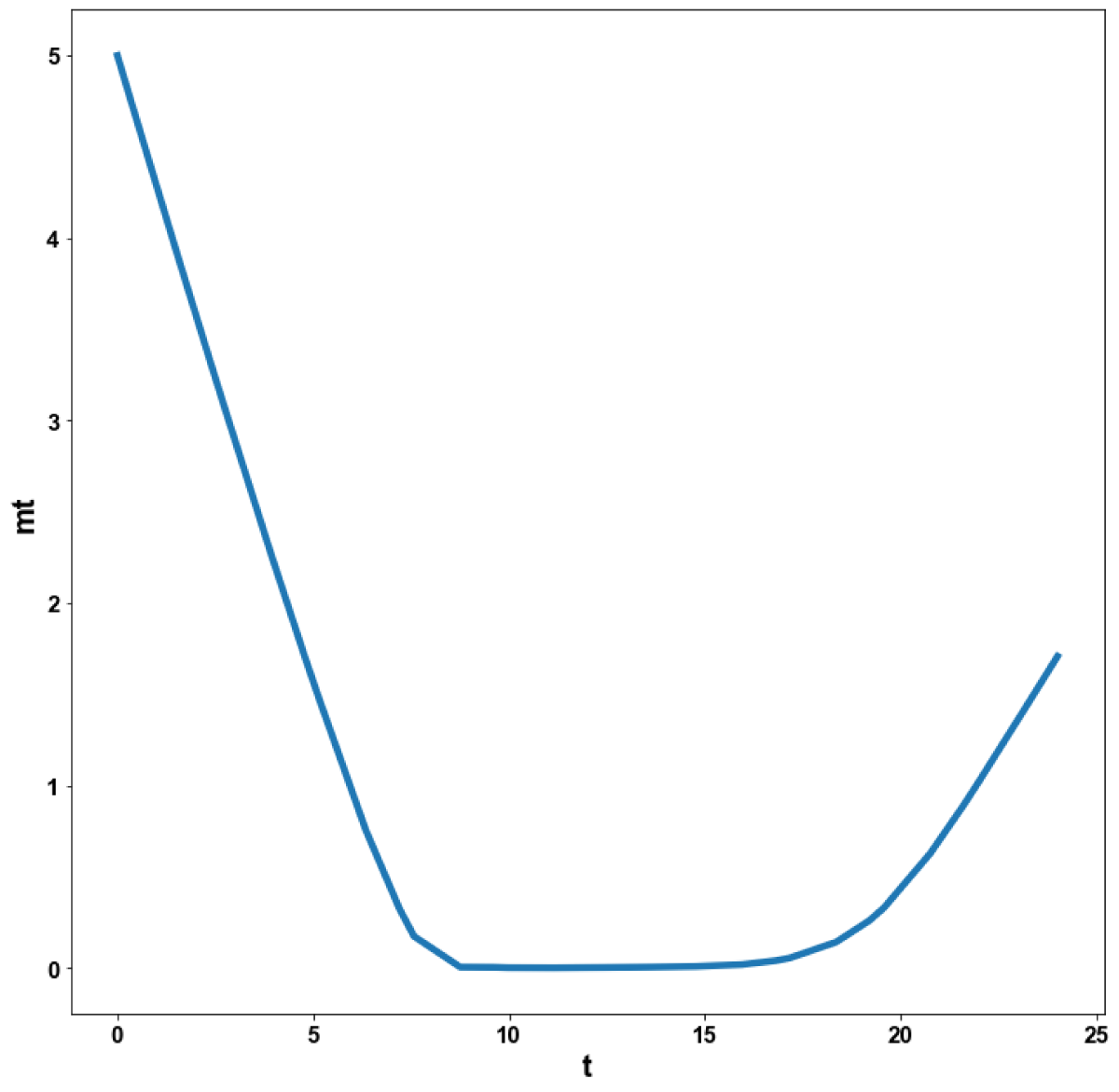
When kdN was the bifurcation parameter the Hopf bifurcation point was found at the point x = (Mp, P0, P1, P2, MT, T0, T1, T2, C, CN, kdN) = (3.291832 1.453513 1.441881 1.434564 3.291832 1.453513 1.441881 1.434564 2.175841 0.816001 1.399881). The limit resulting from this Hopf bifurcation point is shown in Figure 2a. The Hopf bifurcation point and the limit cycle disappeared when kdN was modified to kdN tanh(kdN) / 40 (Figure 2b) When vmP was the bifurcation parameter 2 Hopf bifurcation points was found at x = (Mp, P0, P1, P2, MT, T0, T1, T2, C, CN, vmP) = (0.546958 0.149307 0.138973 0.062696 2.117375 0.760434 0.880921 2.514633 0.296267 0.846478 0.894904) and at (0.410086 0.109841 0.101970 0.043180 2.179160 0.795708 0.957074 3.642237 0.295544 0.844413 0.980167). The limit cycles resulting from these Hopf bifurcation points are shown in Figures 3a and 3b. The Hopf bifurcation points and the limit cycles disappeared when vmP was modified to vmP tanh(vmP) / 320 (Figure 3c). For the MNLMPC calculations (ksP, kdN, vmP) were the time-dependent control variables while the other parameters were the base values. was minimized first and the minimum value obtained was zero. Then was maximized and the resulting maximum value was 10. The objective function for the MNLMPC minimized was . The first obtained control values of (ksP, kdN, vmP) was implemented, the remaining discarded and the procedure was repeated until there was no difference between the implemented and the first obtained control values. These are the MNLMPC control values. When no activation factor was used, the MNLMPC control values were (ksP, kdN, vmP) = (1.4140861276802486 0.9640332102915072 0.6100640938226989).when ksP was modified to ksP tanh(ksP) / 10 when kdN was modified to kdN tanh(kdN) / 40 and when vmP was modified to vmP tanh(vmP) / 320, and the same procedure was followed, the resulting MNLMPC control values were (ksP, kdN, vmP) = (4.999999140881666, 0.0013130511044215727, 4.9999568900984945). Figures 4a-4f show the various MNLMPC profiles when no activation factor was used. The profiles obtained when ksP was modified to ksP tanh(ksP) / 10 when kdN was modified to kdN tanh(kdN) / 40 and when vmP was modified to vmP tanh(vmP) / 320 are shown in Figures 5a-5f. Figures 4c, 4d, and 4e show spikes in the control profiles. These spikes disappeared when the activation factor with the tanh function was implemented. The tanh activation function is used in neural nets (Dubey, et al. [56]; Kamalov, et al. [57] and Szandała) and [58] optimal control problems (Sridhar [59]) to eliminate spikes in the optimal control profile. The tanh factor effectively eliminates spikes that occur in control profiles. Hopf bifurcation points cause oscillatory behavior. Oscillations are similar to spikes and the results demonstrate that the tanh factor also eliminates the Hopf bifurcation by preventing the occurrence of oscillations. Sridhar [60] explained with several exampleshow the activation factor involving the tanh activation function (where a bifurcation parameter u is replaced by (u tanh u/ε) successfully eliminates the limit cycle causing Hopf bifurcation points.
Figure 2a: Limit cycle when kdn is the bifurcation parameter.
Figure 2b: Hopf bifurcation point and limit cycle disappears when kdn is modified to kdn(tanh(kdn))/40.
While intermediate periodic oscillations in Circadian rhythm models have been shown, this article demonstrates that Hopf bifurcations cause these intermediate periodic oscillations. It is also shown that these Hopf bifurcations can be eliminated using the tanh activation factor. The spikes in the control profiles are also eliminated by the same activation factor.
Figure 3a: First Limit cycle when vmp is the bifurcation parameter.
Figure 3b: Second Limit cycle when vmp is the bifurcation parameter.
Figure 3c: Both limit cycles disappear when vmp is modified to vmp tanh(vmp)/320.
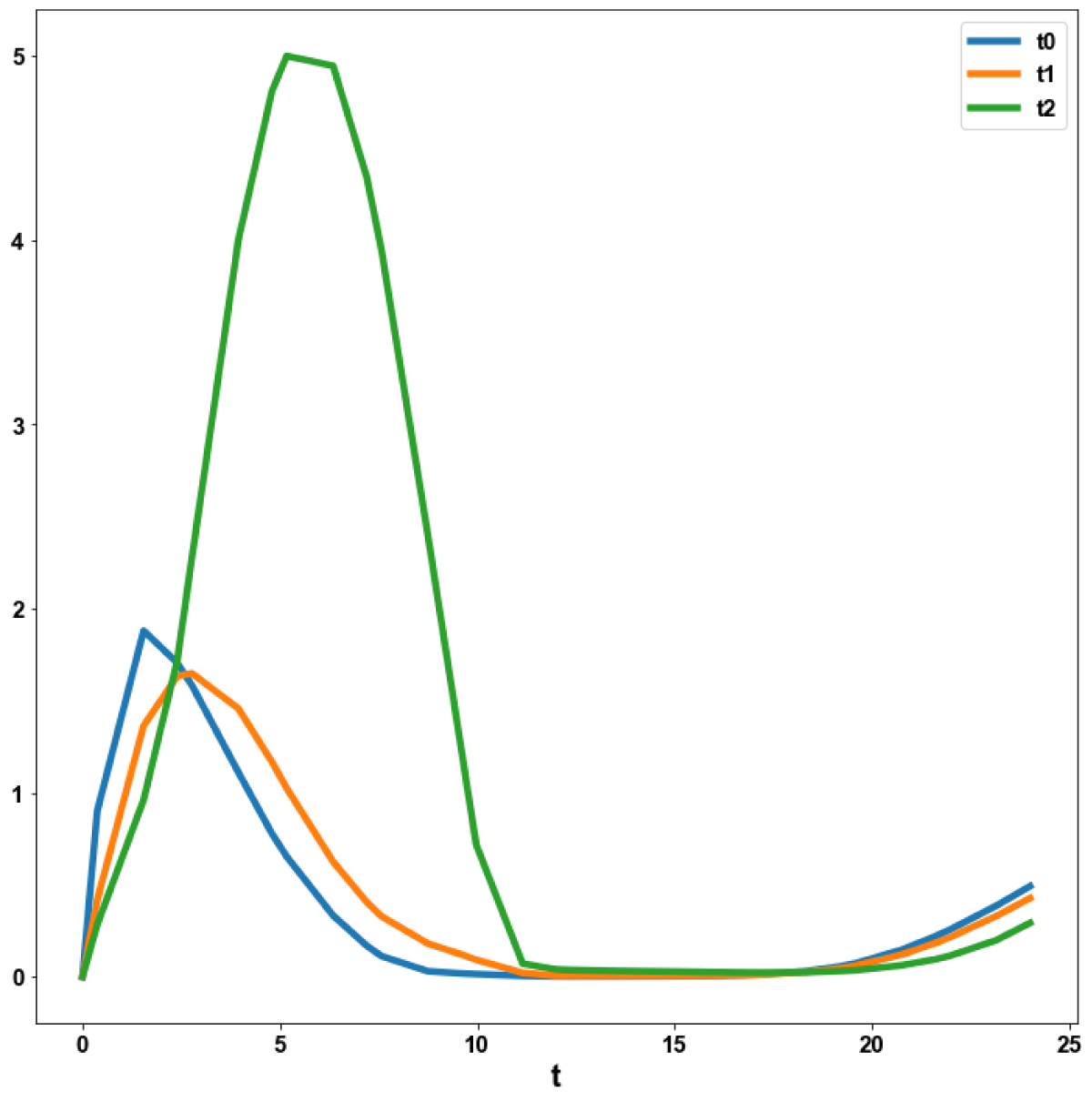
Figure 4a: MNLMPC calculation t0, t1, t2 vs. t no activation factor used.
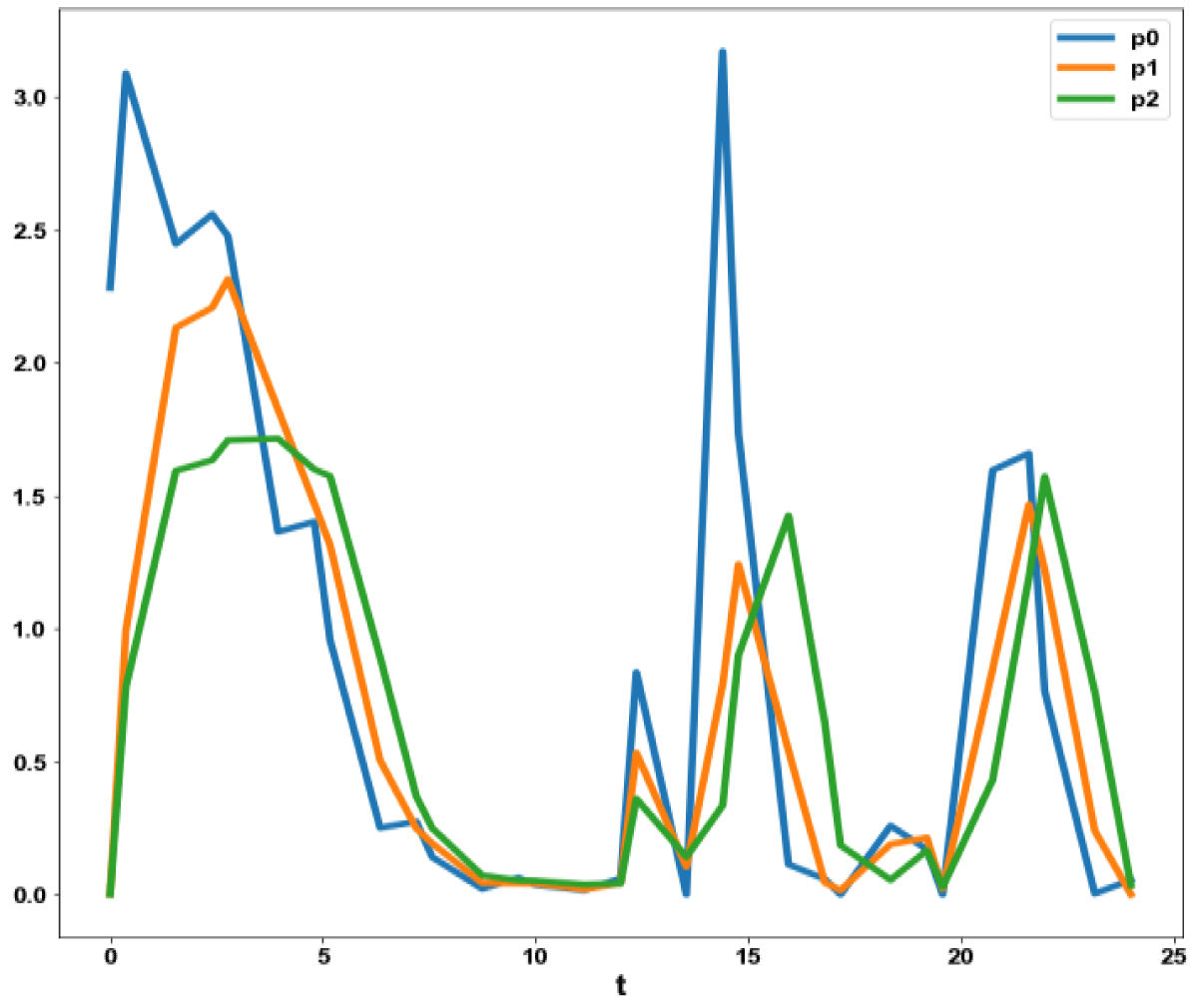
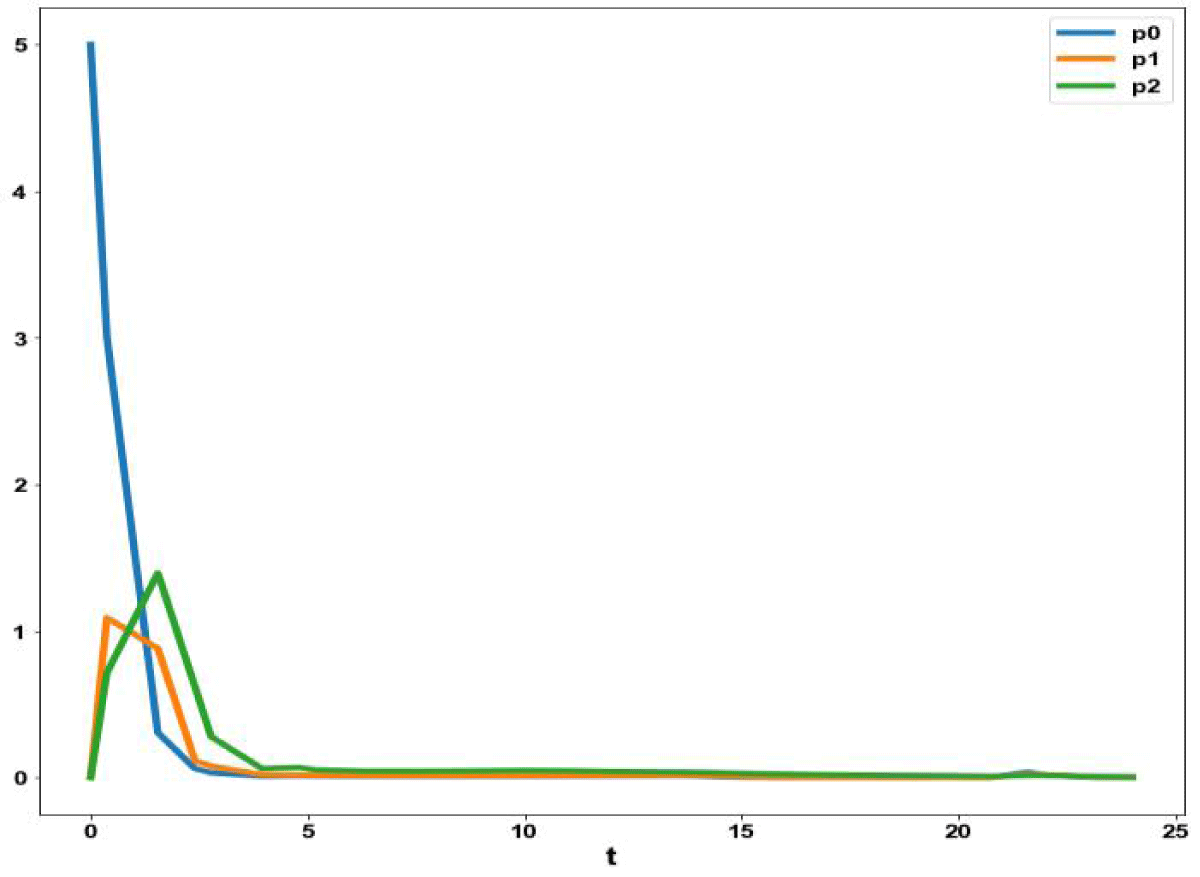
Figure 4b: MNLMPC calculation P0, P1, P2 vs. t no activation factor used.
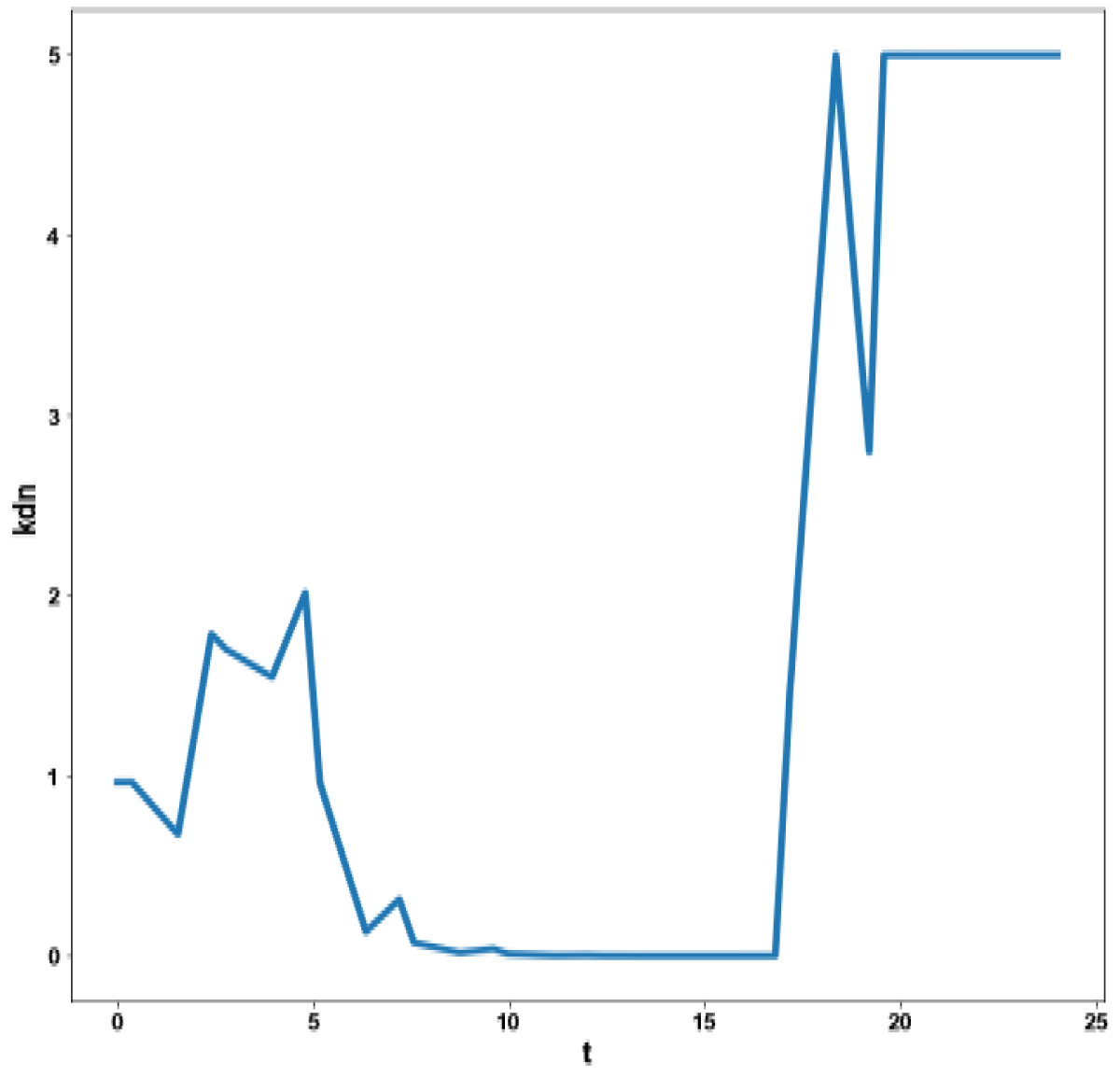
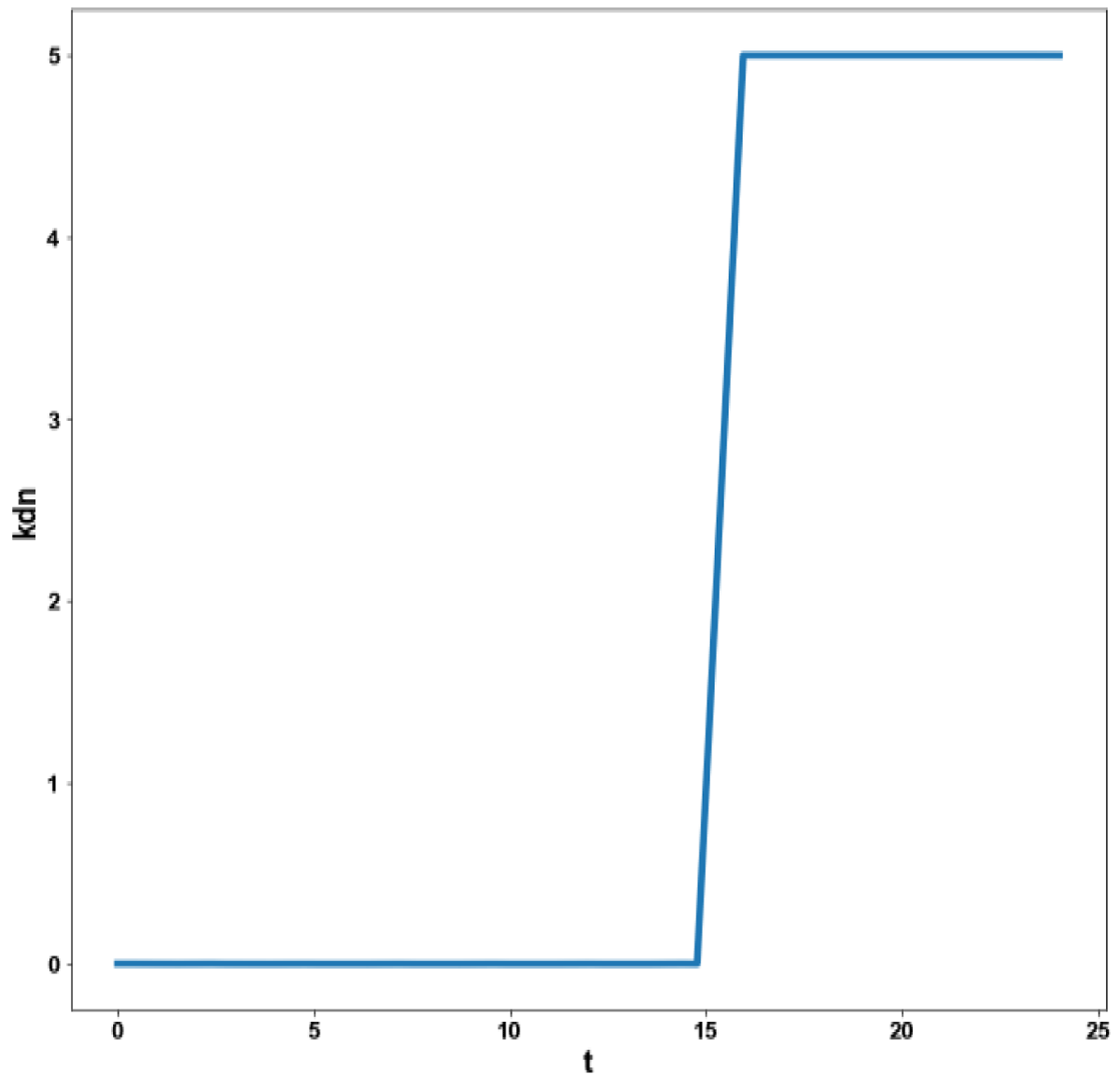
Figure 4c: MNLMPC calculation kdm vs. t no activation factor used.
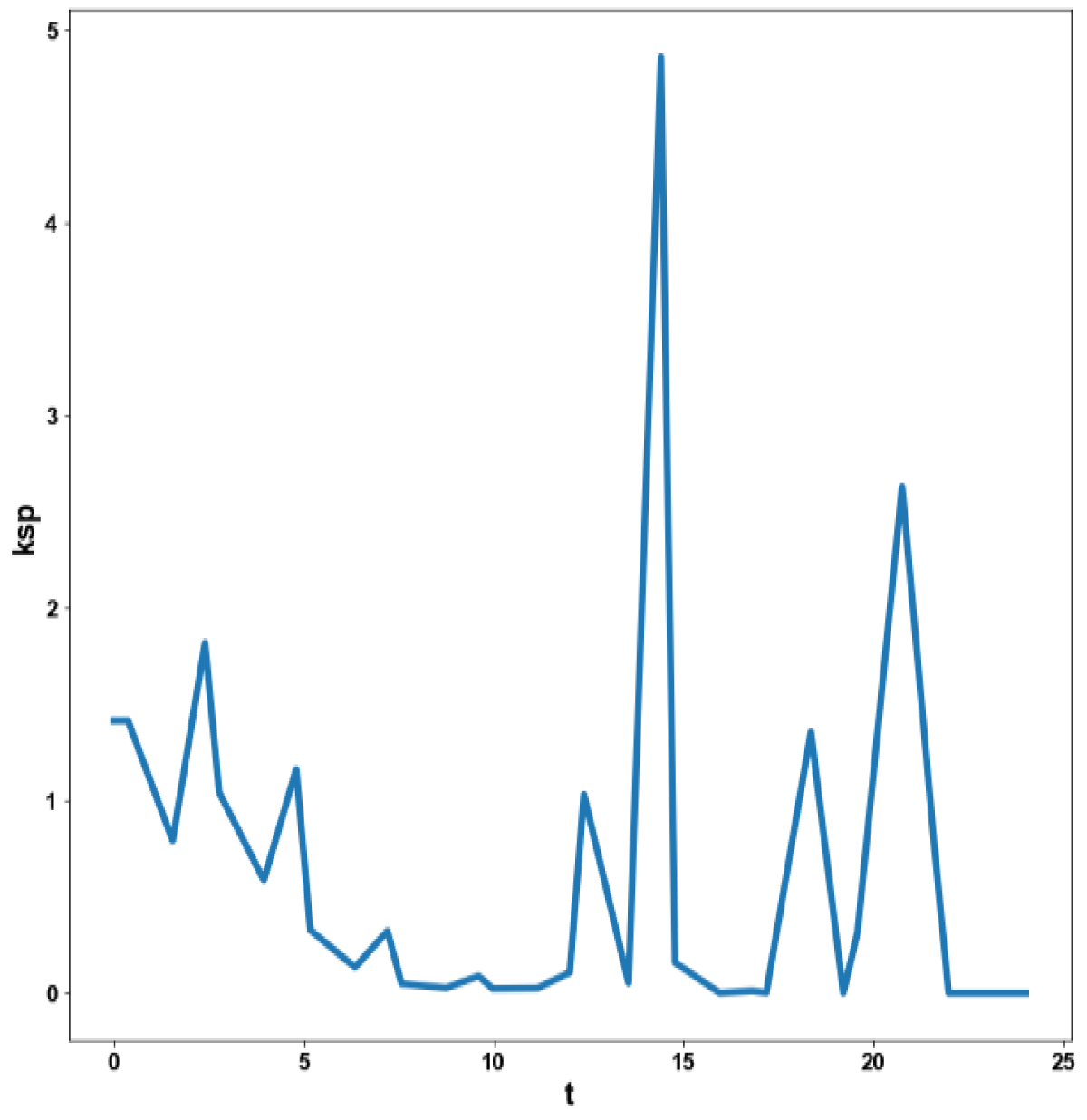
Figure 4d: MNLMPC calculation ksp vs. t no activation factor used.
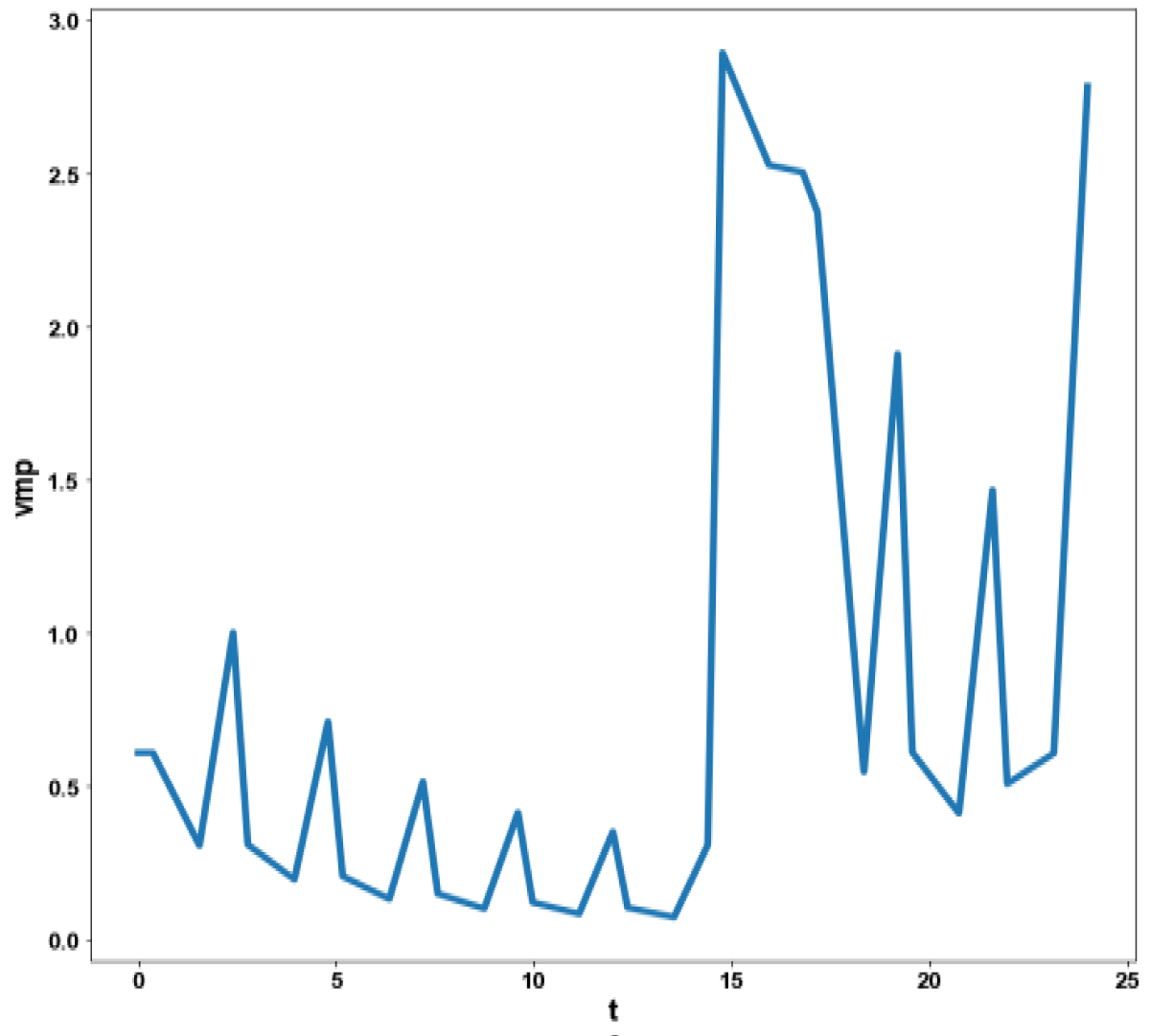
Figure 4e: MNLMPC calculation vmp vs. t no activation factor used.
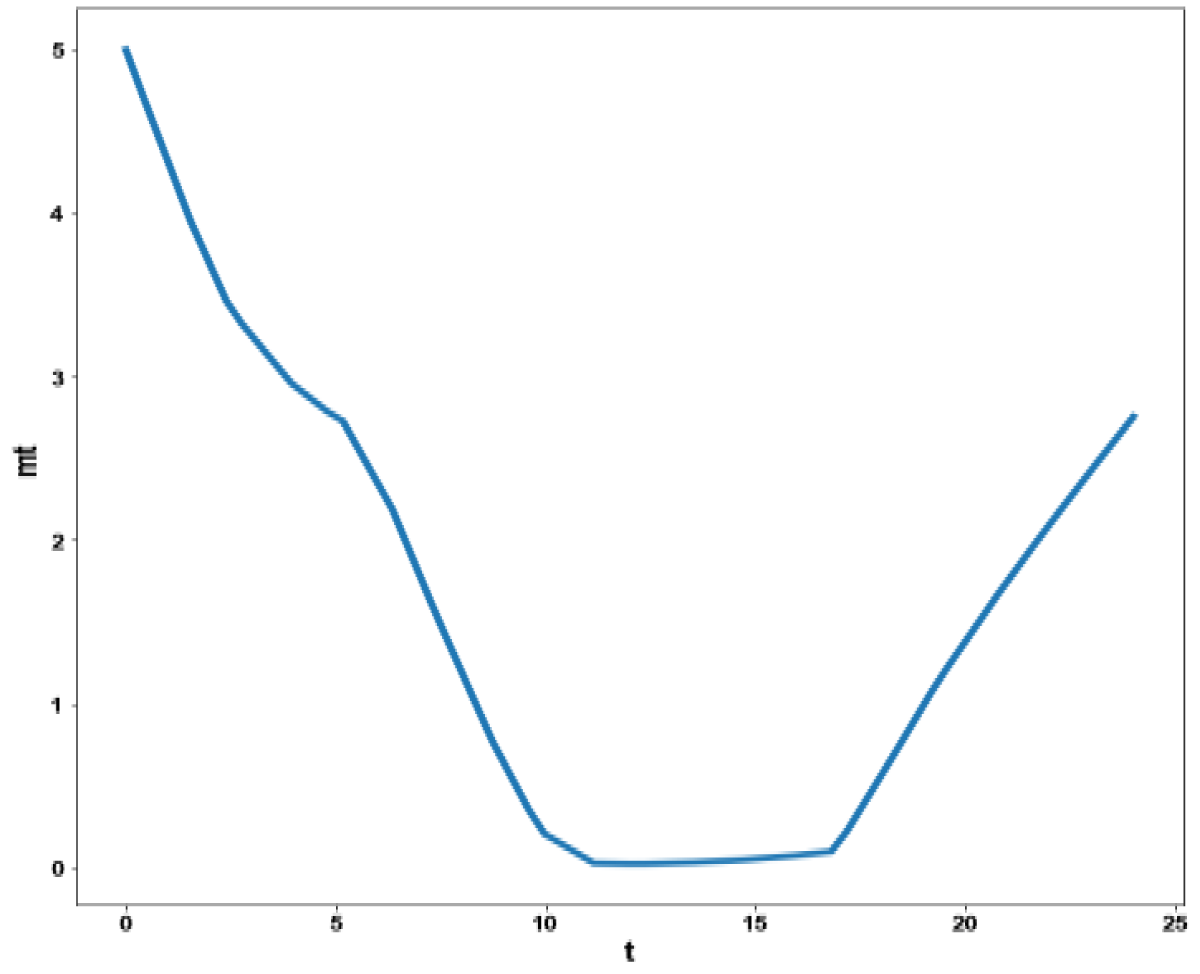
Figure 4f: MNLMPC calculation mt vs. t no activation factor used.
Figure 5a: MNLMPC calculation T0, T1, T2 vs. t with activation factor.
Figure 5b: MNLMPC calculation P0, P1, P2 vs. t with activation factor.
Figure 5c: MNLMPC calculation kdm vs. t with activation factor.
Figure 5d: MNLMPC calculation ksp vs. t with activation factor.
Figure 5e: MNLMPC calculation vmp vs. t with activation factor.
Figure 5f: MNLMPC calculation mt vs. t with activation factor.
Figure 5f: MNLMPC calculation mt vs. t with activation factor.
This work shows that intermediate Hopf bifurcations that cause limit cycles can occur in circadian models involving the period (PER) and timeless (TIM) proteins in Drosophila. Furthermore, the Hopf bifurcation points also cause spikes in the control profiles when Multiobjective nonlinear model predictive calculations are performed. These spikes make control tasks difficult. This research demonstrates that when an activation factor involving the tanh function is used, the oscillation causing Hopf bifurcations and the spikes in the control profiles are eliminated.
- Decroly O, Goldbeter A. Birhythmicity, chaos, and other patterns of temporal self-organization in a multiply regulated biochemical system. Proc Natl Acad Sci U S A. 1982;79(22):6917-21. Available from: https://doi.org/10.1073/pnas.79.22.6917
- Alamgir M, Epstein IR. Birhythmicity and compound oscillations in coupled chemical oscillators: Chlorite-bromate-iodide system. J Am Chem Soc. 1983;105:2500-2501. Available from: https://pubs.acs.org/doi/10.1021/ja00346a080
- Aronson BD, Johnson KA, Loros JL, Dunlap JC. Negative feedback defining a circadian clock: Autoregulation of the clock gene frequency. Science. 1994;263:1578-1584. Available from: https://doi.org/10.1126/science.8128244
- Baylies MK, Weiner L, Vosshall LB, Saez L, Young MW. Genetic, molecular, and cellular studies of the per locus and its products in Drosophila melanogaster. In: Young MW, editor. Molecular Genetics of Biological Rhythms. New York: M. Dekker; 1993. p. 123-153.
- Crosthwaite SK, Dunlap JC, Loros JL. Neurospora wc-1 and wc-2: Transcription, photoresponses, and the origins of circadian rhythmicity. Science. 1997;276:763-769. Available from: https://doi.org/10.1126/science.276.5313.763
- Curtin KD, Huang ZJ, Rosbash M. Temporally regulated nuclear entry of the Drosophila period protein contributes to the circadian clock. Neuron. 1995;14:365-372. Available from: https://doi.org/10.1016/0896-6273(95)90292-9
- Dunlap JC. Genetic and molecular analysis of circadian rhythms. Annu Rev Genet. 1996;30:579-601. Available from: https://doi.org/10.1146/annurev.genet.30.1.579
- Edery I, Rutila JE, Rosbash M. Phase shifting of the circadian clock by induction of the Drosophila period protein. Science. 1994;263:237-240. Available from: https://doi.org/10.1126/science.8284676
- Edery I, Zwiebel LJ, Dembinska ME, Rosbash M. Temporal phosphorylation of the Drosophila period protein. Proc Natl Acad Sci USA. 1994;91:2260-2264. Available from: https://doi.org/10.1073/pnas.91.6.2260
- Edmunds LN. Cellular and Molecular Bases of Biological Clocks: Models and Mechanisms for Circadian Timekeeping. New York: Springer-Verlag; 1988.
- Eskin A, Yeung SJ, Klass MR. Requirement for protein synthesis in the regulation of a circadian rhythm by melatonin. Proc Natl Acad Sci USA. 1984;81:7637-7641. Available from: https://doi.org/10.1073/pnas.81.23.7637
- Gekakis N, Saez L, Delahaye-Brown AM, Myers MP, Sehgal A, Young MW, Weitz CJ. Isolation of timeless by PER protein interaction: Defective interaction between timeless protein and long-period mutant perL. Science. 1995;270:811-815. Available from: https://doi.org/10.1126/science.270.5237.811
- Goldbeter A. A model for circadian oscillations in the Drosophila period (PER) protein. Proc Roy Soc Lond B. 1995;261:319-324. Available from: https://doi.org/10.1098/rspb.1995.0153
- Goldbeter A. Biochemical Oscillations and Cellular Rhythms: The Molecular Bases of periodic and Chaotic Behaviour. Cambridge: Cambridge University Press; 1996. Available from: https://www.scirp.org/reference/referencespapers?referenceid=3243994
- Goodwin BC. Oscillatory behavior in enzymatic control processes. Adv Enzyme Regul. 1965;3:425-438. Available from: https://doi.org/10.1016/0065-2571(65)90067-1
- Hall JC. Tripping along the trail to the molecular mechanisms of biological clocks. Trends Neurosci. 1995;18:230-240. Available from: https://doi.org/10.1016/0166-2236(95)93908-g
- Hall JC, Rosbash M. Genes and biological rhythms. Trends Genet. 1987;3:185-191. Available from: https://doi.org/10.1016/0168-9525(87)90231-9
- Hall JC, Rosbash M. Mutations and molecules influencing biological rhythms. Annu Rev Neurosci. 1988;11:373-393. Available from: https://doi.org/10.1146/annurev.ne.11.030188.002105
- Hong CI, Tyson JJ. A proposal for temperature compensation of the circadian rhythm in Drosophila based on dimerization of the PER protein. Chronobiol Int. 1997;14:521-529. Available from: https://doi.org/10.3109/07420529709001473
- Huang ZJ, Curtin KD, Rosbash M. PER protein interactions and temperature compensation of a circadian clock in Drosophila. Science. 1995;267:1169-1172. Available from: https://doi.org/10.1126/science.7855598
- Khalsa SBS, Whitmore D, Block GD. Stopping the circadian pacemaker with inhibitors of protein synthesis. Proc Natl Acad Sci USA. 1992;89:10862-10866. Available from: https://doi.org/10.1073/pnas.89.22.10862
- Konopka RJ, Benzer S. Clock mutants of Drosophila melanogaster. Proc Natl Acad Sci USA. 1971;68:2112-2116. Available from: https://doi.org/10.1073/pnas.68.9.2112
- Lee C, Parikh V, Itsukaichi T, Bae K, Edery I. Resetting the Drosophila clock by photic regulation of PER and a PER-TIM complex. Science. 1996;271:1740-1744. Available from: https://doi.org/10.1126/science.271.5256.1740
- Leloup JC, Goldbeter A. Temperature compensation of circadian rhythms: Control of the period in a model for circadian oscillations of the PER protein in Drosophila. Chronobiol Int. 1997;14:511-520. Available from: https://doi.org/10.3109/07420529709001472
- Marrus SB, Zeng H, Rosbash M. Effect of constant light and circadian entrainment of perS flies: Evidence for light-mediated delay of the negative feedback loop in Drosophila. EMBO J. 1996;15:6877-6886. Available from: https://pubmed.ncbi.nlm.nih.gov/9003764/
- Myers MP, Wager-Smith K, Rothenfluh-Hilfiker A, Young MW. Light-induced degradation of timeless and entrainment of the Drosophila circadian clock. Science. 1996;271:1736-1740. Available from: https://doi.org/10.1126/science.271.5256.1736
- Qiu J, Hardin PE. per mRNA cycling is locked to lights-off under photoperiodic conditions that support circadian feedback loop function. Mol Cell Biol. 1996;16:4182-4188. Available from: https://doi.org/10.1128/mcb.16.8.4182
- Rosbash M. Molecular control of circadian rhythms. Curr Opin Genet. 1995;5:662-668. Available from: https://doi.org/10.1016/0959-437X(95)80037-9
- Rutila JE, Zeng H, Le M, Curtin KD, Hall JC, Rosbash M. The timSL mutant of the Drosophila rhythm gene timeless manifests allele-specific interactions with period gene mutants. Neuron. 1996;17:921-929. Available from: https://doi.org/10.1016/S0896-6273(00)80223-8
- Saez L, Young MW. Regulation of nuclear entry of the Drosophila clock proteins period and timeless. Neuron. 1996;17:911-920. Available from: https://doi.org/10.1016/s0896-6273(00)80222-6
- Saunders DS, Gillanders SW, Lewis. Light-pulse phase response curves for the locomotor activity rhythm in period mutants of Drosophila melanogaster. J Insect Physiol. 1994;40:957-968. Available from: https://doi.org/10.1016/0022-1910(94)90134-1
- Sehgal A, Price JL, Man B, Young MW. Loss of circadian behavioral rhythms and per RNA oscillations in the Drosophila mutant timeless. Science. 1994;263:1603-1606. Available from: https://doi.org/10.1126/science.8128246
- So WV, Rosbash M. Post-transcriptional regulation contributes to Drosophila clock gene mRNA cycling. EMBO J. 1997;16:7146-7155. Available from: https://doi.org/10.1093/emboj/16.23.7146
- Taylor WR, Dunlap JC, Hastings JW. Inhibitors of protein synthesis on 80S ribosomes phase shift the Gonyaulax clock. J Exp Biol. 1982;97:121-136. Available from: https://doi.org/10.1242/jeb.97.1.121
- Vosshall LB, Price JL, Sehgal A, Saez L, Young MW. Block in nuclear localization of period protein by a second clock mutation, timeless. Science. 1994;263:1606-1609. Available from: https://doi.org/10.1126/science.8128247
- Young MW, Wager-Smith K, Vosshall L, Saez L, Myers MP. Molecular anatomy of a light-sensitive circadian pacemaker in Drosophila. Cold Spring Harb Symp Quant Biol. 1996;61:279-284. Available from: https://pubmed.ncbi.nlm.nih.gov/9246456/
- Zeng H, Hardin PE, Rosbash M. Constitutive overexpression of the Drosophila period protein inhibits period mRNA cycling. EMBO J. 1994;13:3590-3598. Available from: https://doi.org/10.1002/j.1460-2075.1994.tb06666.x
- Zeng H, Qian Z, Myers MP, Rosbash M. A light entrainment mechanism for the Drosophila circadian clock. Nature. 1996;380:129-135. Available from: https://doi.org/10.1038/380129a0
- Teeple K, Rajput P, Gonzalez M, Han-Hallett Y, Fernández-Juricic E, et al. High fat diet induces obesity, alters eating pattern and disrupts corticosterone circadian rhythms in female ICR mice. PLoS ONE. 2023;18:e0279209. Available from: https://doi.org/10.1371/journal.pone.0279209
- Mia S, Sonkar R, Williams L, Latimer MN, Frayne Robillard I, Diwan A, et al. Impact of obesity on day-night differences in cardiac metabolism. Faseb J. 2021;35:e21298. Available from: https://doi.org/10.1096/fj.202001706rr
- Parcha V, Patel N, Gutierrez OM, Li P, Gamble KL, Musunuru K, et al. Chronobiology of natriuretic peptides and blood pressure in lean and obese individuals. J Am Coll Cardiol. 2021;77:2291–2303. Available from: https://doi.org/10.1016/j.jacc.2021.03.291
- Reitz C, Alibhai FJ, de Lima-Seolin BG, Nemec-Bakk A, Khaper N, Martino TA. Circadian mutant mice with obesity and metabolic syndrome are resilient to cardiovascular disease. Am J Physiol Heart Circ Physiol. 2020;319:H1097–H1111. Available from: https://doi.org/10.1152/ajpheart.00462.2020
- Tobeiha M, Jafari A, Fadaei S, Mirazimi SMA, Dashti F, Amiri A, et al. Evidence for the benefits of melatonin in cardiovascular disease. Front Cardiovasc Med. 2022;9:888319. Available from: https://doi.org/10.3389/fcvm.2022.888319
- Festus ID, Spilberg J, Young ME, Cain S, Khoshnevis S, Smolensky MH, et al. Pioneering new frontiers in circadian medicine chronotherapies for cardiovascular health. Trends Endocrinol Metab. 2024. Available from: https://doi.org/10.1016/j.tem.2024.02.011
- Leloup JC, Goldbeter A. A model for circadian rhythms in Drosophila incorporating the formation of a complex between the PER and TIM proteins. J Biol Rhythms. 1998;13(1):70-87. Available from: https://doi.org/10.1177/074873098128999934
- Dhooge A, Govaerts W, Kuznetsov AY. MATCONT: A Matlab package for numerical bifurcation analysis of ODEs. ACM Trans Math Softw. 2003;29(2):141-164. Available from: https://lab.semi.ac.cn/download/0.28315849875964405.pdf
- Dhooge A, Govaerts W, Kuznetsov YA, Mestrom W, Riet AM. CL_MATCONT: A continuation toolbox in Matlab. 2003:161-166. Available from: https://dl.acm.org/doi/10.1145/952532.952567
- Kuznetsov YA. Elements of applied bifurcation theory. Springer; 1998:112. Available from: https://www.ma.imperial.ac.uk/~dturaev/kuznetsov.pdf
- Kuznetsov YA. Five lectures on numerical bifurcation analysis. Utrecht University; 2009. Available from: https://www.ma.imperial.ac.uk/~dturaev/kuznetsov.pdf
- Govaerts WJ. Numerical Methods for Bifurcations of Dynamical Equilibria. SIAM; 2000. Available from: https://epubs.siam.org/doi/pdf/10.1137/1.9780898719543.fm
- Flores-Tlacuahuac A, Morales P, Riveral Toledo M. Multiobjective nonlinear model predictive control of a class of chemical reactors. Ind Eng Chem Res. 2012;51:5891-5899. Available from: https://pubs.acs.org/doi/abs/10.1021/ie201742e
- Miettinen K. Nonlinear multiobjective optimization. Kluwer International Series; 1999. Available from: https://bayanbox.ir/view/2515773690068372592/Kaisa-Miettinen-Nonlinear-Multiobjective-Optimization.pdf
- Hart WE, Laird CD, Watson JP, Woodruff DL, Hackebeil GA, Nicholson BL, Siirola JD. Pyomo – Optimization modeling in Python. Second Edition. Vol. 67. Available from: https://f.openpdfs.org/E315vrGE5Yy.pdf
- Wächter A, Biegler L. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program. 2006;106:25-57. Available from: https://doi.org/10.1007/s10107-004-0559-y
- Tawarmalani M, Sahinidis NV. A polyhedral branch-and-cut approach to global optimization. Math Program. 2005;103(2):225-249. Available from: https://colab.ws/articles/10.1007%2Fs10107-005-0581-8
- Dubey SR, Singh SK, Chaudhuri BB. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing. 2022;503:92-108. Available from: https://doi.org/10.1016/j.neucom.2022.06.111
- Kamalov AF, Nazir M, Safaraliev AK, Cherukuri R, Zgheib R. Comparative analysis of activation functions in neural networks. In: 2021 28th IEEE International Conference on Electronics, Circuits, and Systems (ICECS); Dubai, United Arab Emirates; 2021. p. 1-6. Available from: http://dx.doi.org/10.1109/ICECS53924.2021.9665646
- Szandała T. Review and comparison of commonly used activation functions for deep neural networks. ArXiv. 2020. Available from: https://doi.org/10.1007/978-981-15-5495-7
- Sridhar LN. Bifurcation analysis and optimal control of the tumor macrophage interactions. Biomed J Sci Technol Res. 2023;53(5):BJSTR. MS.ID.008470. Available from: https://biomedres.us/pdfs/BJSTR.MS.ID.008470.pdf
- Sridhar LN. Elimination of oscillation causing Hopf bifurcations in engineering problems. J Appl Math. 2024;2(4):1826. Available from: https://doi.org/10.59400/jam1826